(Last updated: 11-01-2023)
These have been achieved in the following research fields:
A rigorous foundation of the thermodynamic parameters that govern the formation and/or migration of defects in solids has been made in collaboration with Professor Kessar Alexopoulos and has led to a model that interconnect them with bulk properties. This has been made in a series of several tens of publications mainly in Physical Review B during the '70s and the beginning of '80s. The main results have been compiled in the monograph (that was favourably reviewed in Physics Today, November 1987, pp95-96): P. Varotsos and K. Alexopoulos, Thermodynamics of Point Defects and their relation with the bulk properties (North Holland, 1986). [Times cited: several hundred]
The presence of aliovalent impurities in ionic solids results in the formation of extrinsic defects (e.g. vacancies, interstitials) a significant portion of which are placed near the impurities, thus forming electric dipoles relaxation time depends on pressure (stress). Varotsos and Alexopoulos showed that when the pressure reaches a critical value, σcr, a cooperative orientation of these dipoles may occur, which results in the emission of a transient electric signal. This may happen before an earthquake (critical point) since the stress gradually increases in the focal region before the rupture. Along this direction, a detailed experimentation started in Greece in 1981, which showed (P. Varotsos and K. Alexopoulos, Tectonophysics 110, 73-98, 1984; Tectonophysics 110, 99-125, 1984) that actually transient variations of the electric field of the Earth are observed before the occurrence of earthquakes. These signals are termed Seismic Electric Signals, SES (of the so called VAN earthquake prediction method; VAN comes from the initials of Varotsos, Alexopoulos and Nomikos). The results have been published in a series of more than 130 papers during 1984-2013 in refereed journals and arouse a great interest in the international scientific community as it is evident from the following facts:
(i) A meeting, under the title “A critical review of VAN” was held jointly by the International Council of Scientific Unions (ICSU) and the Royal Society at the Society’s London premises on 11-12 May 1995. Sir James Lighthill presided over this meeting in his capacity as Chairman of ICSU's Special Committee for the United Nations' -designated International Decade for Natural Disaster Reduction, 1990-99. The proceedings of this meeting have been published in the book: “A Critical Review of VAN”, Earthquake prediction from seismic electric signals, edited by Sir J. Lighthill, World Scientific, Singapore, 1996.
Other international workshops focused on our research have been organized by:
The proceedings of this conference have been published in Tectonophysics, vol. 224, pp 1-288, August 30, 1993 and forty four researchers from various countries (USA, Russia, Japan, Sweden, France, Poland, Italy etc) participated including the following Institutes: Earthquake Research Institute University of Tokyo, Seismological Dept. Uppsala University, Commissariat à l'Energie Atomique France, Institute of Geophysics Polish Academy of Sciences, University of Illinois at Urbana Champaign, University of North Carolina, Institute of Physics of the Earth, Moscow.
(ii) A special issue of Geophysical Research Letters (Vol. 23, No.11, May 27, 1996) solely focused on our results under the title “Debate on VAN”.
(iii) An article under the title "Quake Prediction Tool Gains Ground" (by Richard A. Kerr), devoted to VAN, was published in Science [270, 911-912 (1995)] and described the development of the method by explaining the successful prediction by the VAN method of the three large earthquakes that occurred in Greece during 1995.
The results of the 25 year period 1981-2005 have been compiled in the monograph: “P. Varotsos, The Physics of Seismic Electric Signals (TerraPub, Tokyo, 2005)”.
The main properties of SES could be summarized as follows (P. Varotsos and K. Alexopoulos, Tectonophysics 110, 73-98, 1984; Tectonophysics 110, 99-125, 1984): First, the SES amplitude is interrelated with the magnitude of the impending earthquake. This interrelation is in fact a power-law which corroborates that the approach of a system to a critical point (second order phase transition) is accompanied by fractal structure, thus being in accordance with the original SES generation mechanism proposed by Varotsos and Alexopoulos. Second, SES cannot be observed at all points of the Earth's surface but only at certain points called “sensitive points”. Each sensitive station enables the collection of SES only from a restricted number of seismic areas (“selectivity effect”). A map showing the seismic areas that emit SES detectable at a given station is called “selectivity map of this station”. This allows the determination of the epicenter of an impending earthquake (e.g. P. Varotsos and M. Lazaridou, Tectonophysics 188, 321-347, 1991; P. Varotsos, K. Alexopoulos and M. Lazaridou Tectonophysics 224, 1-37, 1993). Third, at epicentral distances of the order of 100km, the SES electric field precedes markedly (~1s) the time-derivative of the relevant magnetic field variations [P. Varotsos et al., Phys. Rev. Lett 91, 148501 (2003)]. This, which has been commented on by Physics World-Web of Science of the Institute of Physics (IoP, UK, February 2004), finds applications in the determination of the epicenter of the impending earthquake as well as in the distinction of true SES from “noise” emitted from manmade sources. The physical properties of SES can be theoretically explained, if we take into account the aforementioned SES generation mechanism together with the existence of inhomogeneities in the Solid Earth’s Crust (for a review see “P. Varotsos, The Physics of Seismic Electric Signals (TerraPub, Tokyo, 2005)”). The SES collection from the real time VAN telemetric network (which nowadays consists of 9 measuring stations) enables the estimation of the three parameters: time (see also below the methodology of natural time), epicenter and magnitude of the impending mainshock. These predictions, when the expected magnitude is 6 units or larger, are submitted for publication in scientific journals before the earthquake occurrence. In these cases SES activities are recorded (a SES activity comprises several SES recorded within a short time and appears approximately a few months before a major earthquake).
A new concept of time, termed natural time, was introduced by P. Varotsos, N. Sarlis and E. Skordas, Practica of Athens Academy 76, 294-321, 2001; Phys. Rev. E 66, 011902, 2002. This was followed by a sequence of papers published mainly in Physical Review and Physical Review Letters. The results of the new analysis of experimental results in natural time during the period 2010-2011 have been compiled in a monograph published in 2011 by Springer: Varotsos P. et al., Natural Time Analysis: The new view of time. Precursory Seismic Electric Signals, Earthquakes and other Complex Time Series, Berlin, Heidelberg (2011), 476 pages. In particular, during this decade, it has been found that novel dynamical features hidden behind time series in complex systems can emerge upon analyzing them in the new time domain of natural time, which conforms to the desire to reduce uncertainty and extract signal information as much as possible [Phys. Rev. Lett. 94, 170601 (2005)]. The analysis in natural time enables the study of the dynamical evolution of a complex system and identifies when the system approaches a critical point. Hence, natural time plays a key role in predicting impending catastrophic events in general. Relevant examples of data analysis in this new time domain have been presented during 2001-2011 in a large variety of fields including Medicine, Biology, Earth Sciences and Physics:
First, in Cardiology, natural time analysis of electrocardiograms: Sudden cardiac death (SCD) is a frequent cause of death and may occur even if the electrocardiogram seems to be strikingly similar to that of a healthy individual. Upon employing, however, the entropy defined in natural time, SCD can be clearly distinguished from the truly healthy individuals [P. Varotsos et al., Phys. Rev. E 70, 011106 (2004); Phys. Rev. E 71, 011110 (2005)]. This finding has been commented on by New Scientist (3 April 2004). In addition, when considering the entropy change ΔS under time reversal, not only the SCD risk can be identified, but also an estimate of the time of the impending cardiac arrest can be provided [P. Varotsos et al., Appl. Phys. Lett. 91, 064106 (2007)]. In particular, it was found that the entropy change ΔS3 under time reversal, at the scale of 3 heartbeats (high frequency band of the electrocardiogram), identifies the SCD risk and distinguishes SCD from truly healthy individuals as well as from CHF. As for the entropy change ΔS13 under time reversal at the scale of 13 heartbeats (low frequency band of the electrocardiogram), the appearance of its minimum reveals that the ventricular fibrillation onset is approaching (within a few hours, or so). The use of the quantity ΔS is based on the following concept: SCD can be considered as a phase change (dynamic phase transition) between the following two phases: living systems are examples of systems operating far from equilibrium that are characterized by time irreversibility related to the unidirectionality of the energy flow across the boundaries of the system. In contrast, death is a state of maximum equilibrium since there are no driving forces or consumption of energy, thus being more time reversible than those representing far from equilibrium healthy physiology. Hence SCD can be considered as a phase change (dynamic phase transition) in which a considerable change ΔS of the entropy S is expected. ΔS at specific scales was also found of key importance in the same article to distinguish healthy individuals from congestive heart failure patients.
Second, in Earth Sciences, the SES activities exhibit scale invariance over five orders of magnitude, which agrees with the original proposal that SES are governed by critical dynamics. The natural time analysis also showed that all the measured SES activities are characterized by very strong memory and fall on a universal curve [P. Varotsos et al., Practica of Athens Academy 76, 294-321 (2001); Phys. Rev. E 66, 011902 (2002)]. As for the SES distinction from similar looking “noise”, this is achieved upon employing modern tools of Statistical Physics (detrended fluctuation analysis, wavelet analysis etc.), but applied to the natural time domain [P. Varotsos et al., Phys. Rev. E 67, 021109 (2003); Phys. Rev. E 68, 031106 (2003)].
Third, in Seismology, natural time enables the determination of the occurrence time of an impending major earthquake since, as mentioned, it can identify when a complex system approaches a critical point. Since the detection of an SES activity signifies that the system enters in the critical regime, the small earthquakes that occur after the SES detection are analyzed in natural time. It was found that the variance (κ1) of natural time χ, i.e., κ1=<χ2>-<χ>2, becomes equal to 0.070 (which manifests the approach to the critical point) a few hours to one week before the main shock. This has been ascertained to date for several main shocks in Greece [P. Varotsos et al., Phys. Rev. E 72, 041103 (2005); Phys. Rev. E 73, 031114 (2006)] and Japan [S. Uyeda et al., J. Geophys. Res. 114, B02310 (2009)], including the prediction of three major earthquakes that occurred in Greece during 2008. For example, the 6.9 earthquake on 14 February 2008, which is the strongest earthquake that occurred in Greece during the last 35 years, was publicly announced as imminent on February 10, 2008 along with the identification of its epicenter and magnitude. This arouse a considerable international interest, e.g., see the two recent articles by Japanese scientists in EOS Transactions of the American Geophysical Union [S. Uyeda and M. Kamogawa, EOS 89, No. 39, p.363, 23 September 2008; EOS 91, No. 18, p.162, 4 May 2010]. Upon studying in natural time the fluctuations of the parameter κ1 of seismicity when a natural time window of constant length (i.e., comprising a constant number of events) is sliding event by event through a seismic catalog, the following is found [P. Varotsos et al., Europhys. Lett., EPL 96, 59002 (2011)]: When this number is comparable with the number of earthquakes occurring within a few months (which is on average equal to the lead time of SES activities), the fluctuations of κ1 exhibit a minimum a couple of months before a major earthquake. This fact has been repeatedly confirmed before major earthquakes in various seismic regions (California, Greece, Japan) which supports the aforementioned model for SES generation. In addition, this criticality model foresees that the initiation of an SES activity should be accompanied by the simultaneous appearance of other precursory phenomena, e.g., Earth's surface displacements with specific orientations of the horizontal azimuths, termed GPS azimuths. This has been recently confirmed [P. Varotsos et al., Ann. Geophys. 37, 315-324 (2019)] by observed phenomena before the giant Tohoku earthquake of magnitude MW9.0 on 11 March 2011 in Japan, as it will be further discussed in more detail later.
Fourth, in Statistical Physics, upon employing natural time analysis, a striking similarity of fluctuations in equilibrium critical phenomena and non-equilibrium systems emerges. In particular, it was found [P. Varotsos et al., Phys. Rev. E 72, 041103 (2005)] that the scaled distributions fall on the same curve, which exhibits over four orders of magnitude features similar to those in several equilibrium critical phenomena (e.g., two-dimensional Ising model) and in non-equilibrium systems (e.g., three dimensional turbulent flow). After introducing an order parameter for seismicity, which is the quantity κ1 mentioned above, it was also shown that the worldwide seismicity, as well as that of the San Andreas fault system (California) and Japan fall on the same curve. Furthermore, the b-value (»1) in the Gutenberg-Richter law for earthquakes [stating that the number N (>M) of earthquakes larger than M is given by (N>M) ~ 10-bM] results from natural time analysis by applying the Maximum Entropy Principle. A similar law holds for solar flares etc. [P. Varotsos et al., Phys. Rev. E 74, 021123 (2006)].
Fifth, in Condensed Matter Physics, the time series of the avalanches of the penetration of magnetic flux into thin films of type II superconductors, when analyzed in natural time, were found to obey conditions (as far as the variance and the entropy is concerned) consistent with critical dynamics [N. Sarlis et al., Phys. Rev. B 73, 054504 (2006)]. The same holds for other systems that exhibit the so called self-organized criticality (SOC), e.g., the avalanches in a three dimensional pile of rice getting progressively closer to the critical state.
Sixth, in the Physics of Complex Systems, a challenging point when analyzing data from such systems that exhibit scale invariant structure is the following: In several systems, this non trivial structure points to long range temporal correlations; in other words, the self-similarity results from the process’ memory only (for example, the fractional Brownian motion). Alternatively, the self-similarity may solely result from the process’ increments infinite variance (heavy tails in their distribution). In general, however, the self-similarity may result from both these origins. It has been shown [P. Varotsos et al., Phys. Rev. E 74, 021123 (2006); N. Sarlis et al., Phys. Rev. E 80, 022102 (2009)] that the identification of the origins of self-similarity can be achieved by employing natural time analysis. For example, the original earthquake data exhibit both origins of self-similarity (i.e., temporal and magnitude correlations), while the self-similarity of SES solely comes from infinitely ranged temporal correlations (very strong memory) [P. Varotsos et al., Phys. Rev. E 73, 031114 (2006)].
Several papers have reported SES observations before large earthquakes in Japan [e.g., S. Uyeda et al., Proc. Natl. Acad. Sci. USA 97, 4561-4566 (2000); Proc. Natl. Acad. Sci. USA 99, 7352-7355 (2002); see also Orihara et al., Proc. Natl. Acad. Sci. USA 109, 19125-19128 (2012), which has been highlighted. In particular, Proceedings of the National Academy of Sciences USA (109, 19035, 2012) published a Commentary under the title: “Seismic electrical signals precede earthquakes at Kozu-shima Island, Japan” related with the article of the Japanese workers Y. Orihara et al., Preseismic anomalous telluric current signals observed in Kozu-shima Island, Japan, Proc. Natl. Acad. Sci. USA 109, 19125-19128 (2012). In this article, they analyzed geoelectric field measurements that have been carried out at Kozu-shima Island almost 170 km south of Tokyo during the period 1997-2000. Anomalous electric signals have been recorded which, as also explained in the Commentary, are similar to the SES observed by VAN in Greece since 1981. Furthermore, in this article the Japanese workers based on their experimental results show that the anomalous geoelectric field changes are correlated with the earthquakes far beyond chance, in agreement with the VAN results in Greece. In addition, Japanese workers have applied natural time analysis to SES activities observed in Japan as well as to their subsequent seismicity. They obtained results [Uyeda et al., J. Geophys. Res. 114, B02310 (2009)] which were in striking agreement with those found in Greece.
An additional fact showing the physical interconnection of SES with seismicity has been uncovered in 2013, as follows: Japanese scientists reported [Uyeda et al., Proc. Natl. Acad. Sci. USA 99, 7352-7355 (2002)] that almost 2 months before the onset of the volcanic-seismic swarm activity in the Izu Island region Japan (2000) they measured a pronounced SES activity. This swarm was then characterized by Japan Meteorological Agency as being the largest earthquake swarm ever recorded in Japan. Varotsos et al. [Tectonophysics 589, 116-125 (2013)] demonstrated that a characteristic change of seismicity occurred upon the initiation of the aforementioned SES activity. In particular, the fluctuations of the order parameter κ1 of seismicity simultaneously exhibited a distinct minimum. This is the first time in the literature that well before the occurrence of major earthquakes characteristic changes were found to appear almost simultaneously in two independent datasets of different geophysical observables, i.e., geoelectrical data and seismicity. In addition, Varotsos et al., showed that these two phenomena are also linked in space.
Subsequently, Sarlis et al. (2013) [Proc. Natl. Acad. Sci. USA 110, 13734-13738 (2013)] proceeded to the analysis in natural time of the Japan seismic catalog from 1 January 1984 to 11 March 2011, the day of the super giant Tohoku earthquake of magnitude Mw9.0. They found that the fluctuations of the order parameter of seismicity exhibited distinct minima a few months before all the shallow earthquakes of magnitude 7.6 or larger that occurred during this 27 year period in Japanese area. Among the minima, the minimum before the Mw 9.0 Tohoku earthquake observed on ~5 January 2011 was the deepest. This, by considering the aforementioned findings of Varotsos et al (2013), reflects that a very strong SES activity should have been initiated on the same date. Consequently, anomalous magnetic field changes accompanying the electric field variations of this SES activity should also initiate on this date, i.e., 5 January 2011. This has been strikingly verified by an independent study of Chinese and Japanese scientists [Xu et al., J. Asian Earth Sci. 77, 59-65 (2013)] who reported that anomalous magnetic field variations initiated at a station around 135 km from the Tohoku earthquake epicenter on ~4 January and lasted almost 10 days. The appearance of these anomalous magnetic field variations has been confirmed by analyzing the recordings of a second measuring station as reported in two subsequent papers [Han et al., J Asian Earth Sci. 114, 321-326 (2015) and Han et al., J Asian Earth Sci. 129, 13-21 (2016)]. This phenomenon also happened simultaneously with the development of long range correlations between the earthquake magnitudes of the small seismic events occurring during this period in Japan as found by P. Varotsos et al., [J. Geophys. Res.-Space 119, 9192-9206 (2014)] by applying modern methods of statistical physics, i.e., detrended fluctuation analysis. The development of these long range correlations is consistent with the SES generation mechanism proposed by Varotsos and Alexopoulos, according to which the SES emission occurs at the time at which the system enters the critical stage.
A spatiotemporal study of the minimum of the fluctuations of the order parameter of seismicity unveils an estimate of the epicentral area of an impending major earthquake. This was found in collaboration with Japanese workers as follows: In our earlier study [N. Sarlis et al., Proc. Natl. Acad. Sci. USA 110, 13734-13738 (2013)] by applying natural time analysis of the seismicity mentioned above, we had found that the fluctuations of the order parameter κ1 of seismicity for the entire Japanese region showed a minimum a few months before the shallow major earthquakes (magnitude larger than 7.6) that occurred in the region during the period from 1 January 1984 to 11 March 2011. In a new study [N. Sarlis et al., Proc. Natl. Acad. Sci. USA 112, 986-989 (2015)], by dividing the Japanese areas into small areas, we carry out the calculation of the order parameter fluctuations of seismicity on them. It was found that some small areas show the minimum of these fluctuations almost simultaneously with the larger area and such small areas clustered within a few hundred kilometers from the actual epicenter of the related mainshocks. These results were found to hold for all shallow mainshocks with magnitude 7.6 or larger that occurred in Japan during the aforementioned 27 year period, thus may help estimation of the epicentral location of forthcoming major earthquakes. The Editors of Proc. Natl. Acad. Sci. USA selected this article to be accompanied with a Commentary comprising two pages (by Qinghua Huang, Forecasting the epicenter of a future major earthquake Proc. Natl. Acad. Sci. USA 112, 944-945, 2015) and announced the publication of our article in the cover page of the issue. Based on the preceding spatiotemporal study [N. Sarlis et al., Proc. Natl. Acad. Sci. USA 112, 986-989 (2015)] of the minimum of the order parameter fluctuations of seismicity observed on 5 January 2011, and relying on the previously published estimation of the epicentral location of the forthcoming major earthquake, we analyzed in natural time all the subsequent earthquakes occurring within this candidate epicentral area. The computed κ1 values showed [P. Varotsos et al., Earthq. Sci. 30, 209-218 (2017)] that the critical value κ1=0.070 was approached at 08:36 (local time in Japan) on 10 March 2011, i.e., almost one day before the occurrence of the giant MW9.0 Tohoku earthquake. It is remarkable that this approach happened after the occurrence of the M7.3 earthquake on 9 March 2011, thus showing that this earthquake was a foreshock.In a recent paper by analyzing in natural time the seismicity of the entire Japanese region during the period from 1 January 1984 to the occurrence of the MW9.0 Tohoku earthquake on 11 March 2011, we studied the entropy change ΔS of the entropy S of seismicity upon time reversal [N. Sarlis et al., Europhys. Lett., EPL 124, 29001 (2018) highlighted by EPL]. We found that almost two and a half months before this MW9.0 earthquake a pronounced minimum ΔSmin of ΔS is observed. In particular, this minimum is observed on 22 December 2010 upon the occurrence of the Near Chichi-jima M7.8 earthquake with epicenter at 27.05oN 143.94oE. The robustness of the appearance of this minimum on 22 December 2010 has been assured when changing the earthquake magnitude threshold considered into the calculation, the earthquake depth and the size of the entire Japanese region investigated. These results concerning the existence of ΔSmin before the MW9.0 Tohoku earthquake are in fundamental agreement with our study published in Chapter 8 of our Springer monograph in 2011 concerning the natural time analysis of an earthquake model suggested by Z. Olami, H. Feder and K. Christensen [Phys. Rev. Lett. 68, 1244-1247 (1992)], which is the most studied non-conservative self-organized criticality model. This study has shown that ΔS exhibits a clear minimum before a large avalanche, i.e., before a large earthquake.
In a subsequent paper [P. Varotsos et al., Entropy 20, 757 (2018)] by analyzing the seismicity of Japan in natural time, we found that almost two and a half months before the 2011 MW9.0 Tohoku earthquake, and in particular on the date 22 December 2011, not only the minimum ΔSmin of the quantity ΔS is observed as mentioned in our previous study, but also the fluctuations of ΔS show a considerable increase. In addition, this increase conforms to the theory of phase-transitions suggested by the eminent physicists Lifshitz and Slyozov (1961) and independently by Wagner (1961) exhibiting a scaling relation of the form A(t-t0)c, where the value of the exponent c is c=1/3, the pre-exponential factor A is proportional to the scale (used in the calculation) and t0 was found to be around 0.2 days after the M7.8 earthquake that occurred on 22 December 2010. On the same date mentioned above, i.e., on 22 December 2010, the natural time analysis of the seismicity of Japan revealed [P. Varotsos et. al., Europhys. Lett., EPL 125, 69001 (2019)] that the fluctuations of the order parameter κ1 of seismicity also showed a considerable increase obeying a functional form similar to that found by Penrose and coworkers in 1978 who described the phase transition kinetics following the ideas of Lifshitz and Slyozov (1961). It is remarkable that this functional form of the order parameter fluctuations that we found two and half months before the MW9.0 earthquake in 2011, has not been observed again during the 27 year period studied.On the same date mentioned above, i.e., on 22 December 2010, the natural time analysis of the seismicity of Japan revealed [P. Varotsos et. al., Europhys. Lett., EPL 125, 69001 (2019) also highlighted by EPL] that the fluctuations of the order parameter κ1 of seismicity also showed a considerable increase obeying a functional form similar to that found by Penrose and coworkers in 1978 who described the phase transition kinetics following the ideas of Lifshitz and Slyozov (1961). It is remarkable that this functional form of the order parameter fluctuations that we found two and half months before the MW9.0 earthquake in 2011, has not been observed again during the 27 year period studied.
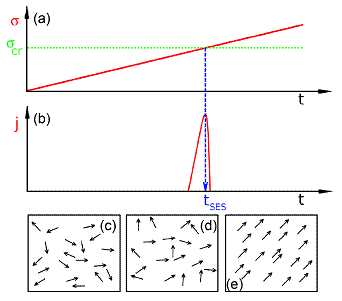
In a very recent work [P. Varotsos et al., Ann. Geophys. 37, 315-324 (2019)] we investigated whether all the above mentioned precursory changes observed before the MW9.0 Tohoku earthquake in 2011, are consistent with the SES generation mechanism suggested by Varotsos and Alexopoulos in the beginning of the 1980s. Before proceeding, and for reader's convenience, we recapitulate this mechanism, as follows (see also the schematic diagram given below): This physical mechanism for SES generation, is termed the “pressure stimulated polarization current (PSPC) model” and suggests the following: In the Earth, electric dipoles always exist due to lattice imperfections in the ionic constituents of rocks. In the future focal region of an EQ, where the electric dipoles have initially random orientations (Fig. c), the stress, σ, starts to gradually increase due to an excess stress disturbance (Fig. a). Let us call this stage A. When this gradually increasing stress reaches a critical value (σcr), the electric dipoles exhibit a cooperative orientation (Fig. e) resulting in the emission of a transient SES (Fig. b) with current density j. (Note that this cooperativity of the electric dipoles constitutes a characteristic property of critical phenomena.) We call this stage B.

Figure: Schematic diagram of the physical mechanism proposed by Varotsos and Alexopoulos in the beginning of the 1980s for the Seismic Electric Signal (SES) generation. (a) Before an earthquake, the stress σ gradually increases in the focal area versus the time t towards reaching a critical value σcr. (b) When σ reaches σcr a transient electric signal (of current density j) is emitted that constitutes an SES. (c) Random orientation of the electric dipoles at small stress. (d) Partial orientation at an intermediate stress σ(< σcr). (e) Cooperative orientation of the electric dipoles when σ= σcr.
Several phenomena of multidisciplinary nature preceded the MW 9 Tohoku earthquake that occurred on 11 March 2011. We find that these phenomena were mainly accumulated around two dates, i.e., 22 December 2010 and 5 January 2011, which concur with the two stages A and B of the PSPC physical model, respectively. These phenomena include the following.a. Around the date 22 December 2010 (stage A):
1. The entropy change of seismicity under time reversal is minimized along with increased fluctuations.2. There is an increase in the fluctuations of the order parameter of seismicity.
3. The horizontal GPS azimuths started to become gradually oriented toward the southern direction (while they had random orientations during the preceding period 12–22 December 2010).
b. Around the date 5 January 2011 (stage B):
1. Anomalous magnetic field variations started (which, according to Maxwell equations, should be accompanied by a strong SES activity).
2. Unprecedented minimum of the fluctuations of the order parameter of seismicity.
3. Full alignment of the orientations of the GPS azimuths southwards.
4. Long-range temporal correlations in the earthquake magnitude time series.
Very recently a procedure has been developed (P. Varotsos et al., Europhys. Lett., EPL, 130, 29001 (2020)) for the identification of the occurrence time of the MW=9.0 Tohoku earthquake that occurred in Japan on 11 March 2011 based on natural time analysis of seismicity. Using the complexity measure that quantifies the fluctuations of the entropy change ΔS of seismicity under time reversal, it was shown that, in the longer scales, the complexity measure of the entire Japanese region starts increasing from 22 December 2010 (the date at which ΔS is minimized) reaching a maximum close to the appearance of a SES activity (evidenced from the recording of anomalous magnetic field variations on the z-component) in the beginning of January 2011; then it gradually diminishes until just before the mega earthquake. On the other hand, around two days before the MW9.0 earthquake occurrence, the complexity measure in the candidate epicentral area exhibits an abrupt increase. This difference reveals, well in advance, that the M7.3 earthquake on 9 March 2011 was a foreshock, which is very important for the following reason: Upon the occurrence of this M7.3 earthquake, seismologists could not identify that this was foreshock of a significantly larger EQ, which would be of paramount importance for practical purposes.
This earthquake struck the Mexico’s Chiapas state. It left dozens dead and destroyed or severely damaged the homes of 2.3 millions or more. Most big Mexico’s earthquakes occur right along the interface between subducting Cocos plate and North American plate. But in this case the earthquake occurred within the Cocos plate itself. Seismologists say this type of faulting would not produce such large earthquakes and this is why characterized it (in several scientific journals including Science and Nature) as an “extremely strange” event and largely “unexpected”. Well before this earthquake occurrence, however, two researchers from Mexico (Ramirez-Rojas and Flores-Marquez) employed natural time analysis and studied Mexico’s seismicity in six tectonic regions (the selection of which was based on tectonic and geological grounds) including the Chiapas region. This study, published in Physica A showed that the probability for the occurrence of a large earthquake was the highest in the Chiapas region (where the above mentioned M8.2 occurred) compared to the five other tectonic regions. This conclusion was further strengthened in a paper [N Sarlis et al., Physica A 506, 625-634 (2018)] we jointly published with Ramirez-Rojas and Flores-Marquez, in which was shown that two key properties of seismicity were obeyed in Chiapas region supporting the conclusion that the occurrence of an extreme event in this region should not be considered unexpected. In the same paper, the entropy change ΔS under time reversal of the seismicity during the 6-year period 2012-2017 in the Chiapas region was studied by using a sliding natural time window comprising a number of events comparable with that occurring on average within the lead time of SES activities. It was found that the quantity ΔS exhibited a clear minimum ΔSmin on 14 June 2017, thus signaling that a major event was impending there, as actually happened almost three months later with the occurrence of the M8.2 earthquake on 7 September 2017. This finding is strikingly similar with the minimum ΔSmin of seismicity found before the giant Tohoku MW9.0 earthquake in 2011 in Japan. In another work jointly published with Ramirez-Rojas and Flores-Marquez [A. Ramirez-Rojas et al., Entropy 20, 477 (2018)] we showed that on the same date, i.e., on 14 June 2017, the fluctuations of ΔS exhibit considerable increase obeying the aforementioned scaling relation suggested by the eminent physicists Lifshitz and Slyozov (1961) and independently by Wagner (1961). In addition, was found [N. Sarlis et al., Physica A 517, 475-483 (2019)] that the temporal correlations between the earthquake magnitudes had different behavior before and after the ΔSmin observation, i.e., while before ΔSmin they exhibited anticorrelation (almost close to random behavior), they turned to long-range correlations after ΔSmin.
In a recent article [N. Sarlis et al., Entropy 21, 301 (2019)] we studied, in collaboration with the aforementioned researchers from Mexico, the fluctuations of the order parameter of seismicity during the 30 year period from 1 January 1988 to the occurrence of the M8.2 earthquake on 7 September 2017. We found that they exhibited a minimum on 27 July 2017, i.e., almost two and a half months before the occurrence of the M8.2 earthquake. Since the appearance of this minimum should be simultaneous with the initiation of an SES activity [P. Varotsos et al., Tectonophysics 589, 116-125 (2013)], we started from this date to compute the κ1 values of seismicity in the Chiapas region and found that the critical condition κ1=0.070 was satisfied upon the occurrence of a M4.2 earthquake at 16:06 UTC on 6 September 2017, thus signaling that the major earthquake was imminent. Actually, next day the M8.2 earthquake occurred.
“We propose to use the idea of nowcasting to answer the question of the current hazard state of the region. More specifically, we count the number of small earthquakes since the last large earthquake in a defined region to estimate the current hazard level in the region. Event counts as a measure of “time,” rather than the clock time, is known as “natural” time [Varotsos et al., 2002, 2005, 2011; Holliday et al., 2006]. We will show that the use of natural time has at least two advantages when applied to earthquake seismicity …”
and in thm description of their procedure the authors explain:
“The basis for our nowcast is the use of “natural” time. Natural time is simply the count of small earthquakes, in our case the number n of small earthquakes since the last large earthquake. The statistical distribution of n will be an essential part of our analysis. There are several advantages to using natural time. The first is that it is not necessary to separate the aftershocks (“decluster”) from the background seismicity. A second is that only the natural interevent count statistics are used rather than the seismicity rate, which involves calendar time as well.”
Several studies in various aspects have been published by means of this method, examples of which are the following:
First, estimation of seismic risk to global megacities [J. B. Rundle, M. Luginbuhl, A. Giguere and D. L. Turcotte, Pure and Applied Geophysics 175, 647-660 (2018)].
Second, investigation of the question whether the large global earthquakes are temporally clustered [M. Luginbuhl, J. B. Rundle and D. L. Turcotte, Pure and Applied Geophysics 175, 661-670 (2018)].
Third, to quantify the temporal evolution of the induced seismicity at the Gronigen gas field in the Netherlands [M. Luginbuhl, J. B. Rundle and D. L. Turcotte, Geophys. J. Int. 215, 753-759 (2018)]. Remarkably the summary of this article ends as follows: “The method utilizes the number of small earthquakes that occur between pairs of large earthquakes. A major advantage of nowcasting is that it relies on ‘natural time’, earthquake counts, between events rather than clock time. Thus, the results are applicable to induced seismicity that varies in time. We count the rate of occurrence of small induced earthquakes to nowcast the probability of occurrence of larger earthquakes.”
Fourth, comparison of induced earthquakes in Oklahoma and at Geysers, California [M. Luginbuhl, J. B. Rundle, A. Hawkins and D. L. Turcotte, Pure and Applied Geophysics 175, 49-65 (2018)].
Fifth, global seismic nowcasting with Shannon information entropy [J. B. Rundle, A. Giguere, D. L. Turcotte, J. P. Crutchfield and A. Donnellan, Earth and Space Science 6, 191-197 (2019)].
Sixth, nowcasting great global earthquakes and tsunami sources [J. B. Rundle, M. Luginbuhl, P. Khapikova, D. L. Turcotte, A. Donnellan and G. McKim, Pure and Applied Geophysics doi:10.1007/s00024-018-2039-y]. In this article, the authors extend the nowcasting method to great earthquakes of magnitude as large as M9. Their main conclusion is the following: The two regions that appear to be at highest current risk for a great earthquake and/or tsunami are the Aleutians East and Kamchatka source regions.
Seventh, nowcasting earthquakes in the Bay of Bengal region [Pasari, S., Pure Appl. Geophys. 176, 1417-1432 (2019)]. Following the Introduction of this paper, we may recapitulate this newly introduced method as follows: “Nowcasting of earthquakes refers to the evaluation of earthquake hazards at the current time, or simply put, determining the amount or the level of seismic progress to the next large event in the earthquake cycle of a region (Rundle et al. 2016, 2018). The idea here is built upon two pieces of vital information. First, it uses the concept of natural time, small earthquake counts between large events, rather than the usual inter-event (clock) time. Second, it considers an ‘‘earthquake cycle’’ as the recurring events in a large seismically active region comprising several active faults, rather than the traditional focus on recurring events on individual faults. While the idea of natural time is unique in its characteristics, the notion of ‘‘earthquake cycle’’ has been applied in many earlier seismology studies (Utsu 1984; Pasari and Dikshit 2015a, b).”
Finally, we note that nowcasting is distinct from forecasting as clarified in the aforementioned paper by Rundle et al. (2016): “Nowcasting, which describes the present state of a system, is distinct from the idea of forecasting, which looks forward in time [Holliday et al., 2005, 2016; Field, 2007; Rundle et al., 2012]. Forecasting is the calculation of probabilities for the future. Nowcasting is the calculation of the current state of the system. Nowcasting can be used as a basis for forecasting if a method is used to project the current state into future states. In fact, nowcasting should be a prerequisite to forecasting, the estimation of the future state of the system. The current state must be known, at least approximately, before the future state can be accurately estimated.”
After 2011 (i.e. the date of the publication of the aforementioned monograph by Springer in 2011), several publications by other authors appeared, based on Natural Time and focusing on forecasting and nowcasting extreme environmental events such as El Niño, cosmic rays, ozone hole, volcanic eruptions, and weather events. These are compiled in Part II of the aforementioned monograph, which is now in press by Springer under the title: Natural Time Analysis: The new view of time, Part II. Advances in Disaster Prediction using Complex Systems (Springer 2023).
In recent years, a technique termed photoelectric plethysmography, also known as photoplethysmography (PPG), has simplified the recording of heart rate in an easy and reliable way. From 1980 the PPG method is used as pulse oximeter for monitoring a person's oxygen saturation into clinical care. Nowadays the PPG technology is included in many modern affordable devices such as smart phones, smart watches, tablets, bracelets, rings etc. It is a simple technique with low cost and gives us health-related information such as heart rate variability (HRV), blood oxygen saturation (SpO2), blood pressure and the respiratory rate.
In a recent work just published [G. Baldoumas, D. Peschos, G. Tatsis, S.K. Chronopoulos, V. Christofilakis, P. Kostarakis, P. Varotsos, N.V. Sarlis, E.S. Skordas, A. Bechlioulis, L.K. Michalis and K.K. Naka, A prototype photoplethysmography electronic device that distinguishes congestive heart failure from healthy individuals by applying natural time analysis. Electronics 8, 1288 (2019)] a prototype PPG electronic device is presented for the distinction of individuals with CHF from the H by applying the concept of NTA. Data were collected simultaneously with a conventional three-electrode ECG system and our prototype PPG electronic device from H and CHF volunteers (99 individuals in total) at the 2nd Department of Cardiology, Medical School of Ioannina, Greece. Our results show a clear separation of CHF from H subjects by means of NTA upon using machine learning techniques, such as support vector machines (SVM), for both the conventional ECG system and our PPG prototype system which additionally inherits the advantages of a low-cost portable device. This is the first work that employs NTA in the complex dynamical system of the heart by using data obtained by a low-cost portable accurate PPG electronic device as well as by ECG and compares the results. Furthermore, the clear distinction of H from CHF individuals may be achieved through a small time window. This method may aid, even when ECG are not available, in the diagnosis of HF syndrome and the identification of CHF patients at higher risk for SCD by means of portable PPG data.
In particular, our database contains simultaneous ECG and PPG recordings from thirty two records from H individuals (9 women and 23 men), aged 24 to 58, and sixty seven records from patients (22 women and 45 men), aged 55 to 87. After data acquisition from both ECG and PPG systems and the completion of the signal processing, we applied NTA for finding the complexity measures Λ7 and Λ49 for each individual. These complexity measures are the fluctuations of the entropy change ΔS under time reversal at the scales 7 and 49 heartbeats, respectively (these scales lie near to the transition from the high frequency band to the low frequency band and from the low frequency band to the very low frequency band of the ECG, respectively), compared to the fluctuations of ΔS at the scale of 3 heartbeats (high frequency band) [Varotsos et al. Appl. Phys. Lett. 91, 064106 (2007); Varotsos P. A., Sarlis N. V. and Skordas E. S., Natural Time Analysis: The new view of time. Precursory Seismic Electric Signals, Earthquakes and other Complex Time-Series (Springer-Verlag, Berlin Heidelberg) 2011 (see page 185); N.Sarlis et al. EPL 109, 18002 (2015)]. In order to optimize the classification between CHF and H, we employed the SVM method, which is a learning machine that can be used for two-group classification even for non-separable data that also avoids computing posterior probabilities. When using the pairs (Λ7, Λ49) and adopting Gaussian radial basis functions in SVM, we obtained the following values of the accuracy A -which is the ratio of the sum of True Positives (TP) plus True Negatives (TN) over the totality of the cases examined: For PPG the value A=93% (one CHF mixes with H and six H mix with CHF), while for ECG the value A=95% (one CHF mixes with H and four H mix with CHF). The comparison of our results with studies of other groups to distinguish a target group comprising of at least 40 CHF from healthy individuals reveals that the sensitivity value (the proportion of the truly identified positives) achieved by our study is 97.7% the highest reported to date.
In summary, the classification between CHF and H was elaborated by using natural time analysis and non-linear radial basis function SVM that led to comparable values of accuracy A for both PPG and ECG. We expect that the employment of this PPG electronic device in the general population due to its simplicity of use could contribute to the detection of underlying heart problems and the timely notification to health care units.